


本案例为挖掘机铲斗与货车尾箱接触的案例。

计算刚度K所需要的参数主要包括接触单元的弹性模量,泊松比以及接触球体半径。本案例为挖掘机的铲斗与矿车尾门的接触,均为钢材料,具体的参数如下:
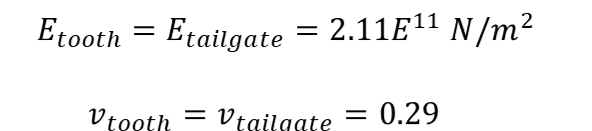
通过上述的输入,可以计算合成弹性模量E*的大小,根据计算公式:
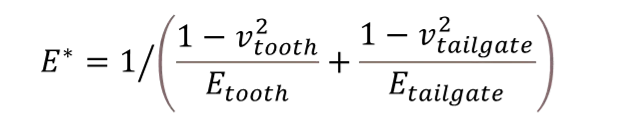
可以计算得到合成的弹性模量E*=1.15E11 N/m2
挖掘机的铲斗与尾门的接触,铲斗接触单元为平面,故Rtooth=∞,而尾箱接触单元为类圆柱形状,Rtailgate=0.1m。根据如下公式:

计算得到等效半径R=0.1m。
根据刚度计算公式:

可以推导出接触刚度K=4.85E10N/m ;对于金属材料的光滑实体,接触指数可初步定义为e=3/2。接触阻尼相对于接触刚度相差两个量级,同时计算的刚度K相比于默认值(默认值为1E8N/m)大两个数量级,故最大阻尼系数的初始值可定义为1E6 N·sec/m,最大渗透深度dmax可初始定义为等效半径R的1%,即dmax=1%*R=0.001m。根据上述各个参数的初始值进行第一次的仿真分析计算。
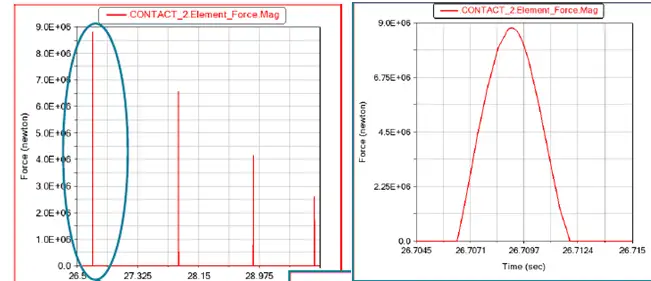
根据垂向接触力、等效半径、合成的弹性模量以及渗透深度计算的公式,可以求解接触过程中的渗透深度。具体公式如下:
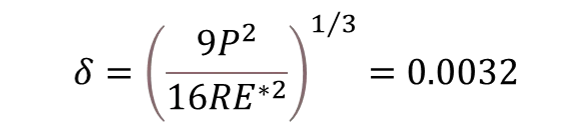
根据上述计算的渗透深度,可以计算出新的最大渗透深度dmax=30%*δ =0.001,根据最新的最大渗透深度进行第二次仿真分析。具体结果如下:
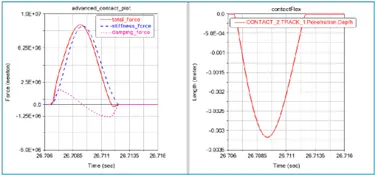
从上图的曲线结果可知,接触力刚度力(8.67E6 N)与阻尼力(1.7E6 N)的比值为5.1:1,相对于理想状态偏差较大(理想的占比关系为阻尼力:刚度力=1:9),故接下来需要调小阻尼系数弱化阻尼力的占比。
为了弱化步骤2中阻尼力的占比,需要将阻尼调小,本文最终将阻尼值调节为6.0E5 N·sec/m。具体的仿真结果如下。

调节好阻尼值后,从上图的曲线结果可知,接触力刚度力(9.27E6 N)与阻尼力(1.04E6 N)的比值为8.94:1,调试结果相对比较理想。
根据步骤3中计算的垂向接触力,根据渗透深度计算的公式,再次计算接触过程中的渗透深度。具体公式如下:
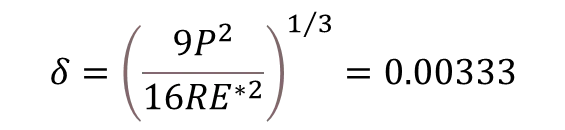
仿真的最大渗透深度为0.0033,相比于计算值相差不大,所以最大渗透深度不再需要调节。
仿真的渗透深度需要接近于手动计算的渗透深度,如果刚度力与阻尼力的占比关系仍不能接受或者求解的最大渗透量不正确,则需要调节刚度部分。而影响刚度力大小的参数主要为刚度和力指数。
1)刚度值主要影响中后段;
2)力指数主要影响起始段。
